Backpack II
Given n items with size A[i] and value V[i], and a backpack with size m. What's the maximum value can you put into the backpack?
假设我们有n件物品,分别编号为1, 2...n。其中编号为i的物品价值为vi,它的重量为wi。为了简化问题,假定价值和重量都是整数值。现在,假设我们有一个背包,它能够承载的重量是W。现在,我们希望往包里装这些物品,使得包里装的物品价值最大化,那么我们该如何来选择装的东西呢?
Example
Given 4 items with size [2, 3, 5, 7] and value [1, 5, 2, 4],
and a backpack with size 10. The maximum value is 9.
Note
You cannot divide item into small pieces and the total
size of items you choose should smaller or equal to m.
Challenge
O(n x m) memory is acceptable, can you do it in O(m) memory?
解题思路
假定我们定义一个函数c[i,w]表示到第i个元素为止,在限制总重量为w的情况下我们所能选择到的最优解。那么这个最优解要么包含有i这个物品,要么不包含,肯定是这两种情况中的一种。如果我们选择了第i个物品,那么实际上这个最优解是c[i - 1, w-wi] + vi。而如果我们没有选择第i个物品,这个最优解是c[i-1, w]。这样,实际上对于到底要不要取第i个物品,我们只要比较这两种情况,哪个的结果值更大不就是最优的么?
另外,对于初始的情况呢?很明显c[0,w]里不管w是多少,肯定为0。因为它表示我们一个物品都不选择的情况。c[i, 0]也一样,当我们总重量限制为0时,肯定价值为0。
这样,基于我们前面讨论的这3个部分,我们可以得到一个如下的递推公式:
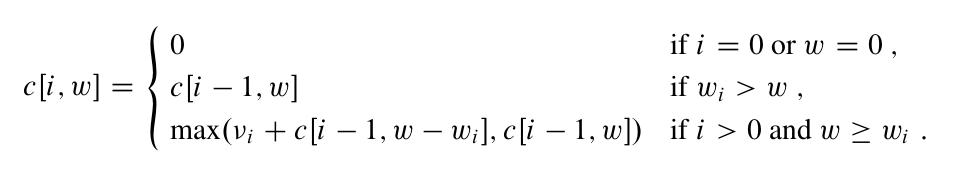
public int backPackII(int m, int[] A, int V[]) {
// write your code here
int[][] d = new int[A.length+1][m+1];
for (int i = 0; i <= A.length; i++) {
for (int j = 0; j <= m; j++) {
if (i == 0 || j == 0) {
d[i][j] = 0;
} else {
if (A[i-1] <= j) {
d[i][j] = Math.max(d[i-1][j], d[i-1][j-A[i-1]] + V[i-1]);
} else {
d[i][j] = d[i-1][j];
}
}
}
}
return d[A.length][m];
}