Find the Duplicate Number(Hard)找到重复数字
题目:Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
Notes:
- You must not modify the array (assume the array is read only).
- You must use only constant, O(1) extra space.
- Your runtime complexity should be less than O(n2).
- here is only one duplicate number in the array, but it could be repeated more than once.
这道题给了我们n+1个数,所有的数都在[1,n]区域内,首先让我们证明必定会有一个重复数,这不禁让我想起了小学华罗庚奥数中的抽屉原理(又叫鸽巢原理)
映射找环法:时间 O(N) 空间 O(1)
假设数组中没有重复,那我们可以做到这么一点,就是将数组的下标和1到n每一个数一对一的映射起来。比如数组是213,则映射关系为0->2, 1->1, 2->3。假设这个一对一映射关系是一个函数f(n),其中n是下标,f(n)是映射到的数。如果我们从下标为0出发,根据这个函数计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推,直到下标超界。实际上可以产生一个类似链表一样的序列。比如在这个例子中有两个下标的序列,0->2->3。
但如果有重复的话,这中间就会产生多对一的映射,比如数组2131,则映射关系为0->2, {1,3}->1, 2->3。这样,我们推演的序列就一定会有环路了,这里下标的序列是0->2->3->1->1->1->1->...,而环的起点就是重复的数。
所以该题实际上就是找环路起点的题,和Linked List Cycle II一样。我们先用快慢两个下标都从0开始,快下标每轮映射两次,慢下标每轮映射一次,直到两个下标再次相同。这时候保持慢下标位置不变,再用一个新的下标从0开始,这两个下标都继续每轮映射一次,当这两个下标相遇时,就是环的起点,也就是重复的数。对这个找环起点算法不懂的,请参考Floyd's Algorithm。
public int findDup(int[] nums) {
int slow = nums[0];
int fast = nums[nums[0]];
//找到快慢指针相遇的地方
while(slow != fast) {
slow = nums[slow];
fast = nums[nums[fast]];
}
//用一个新指针从头开始,直到和慢指针相遇,得到环的起点
fast = 0;
while(slow != fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
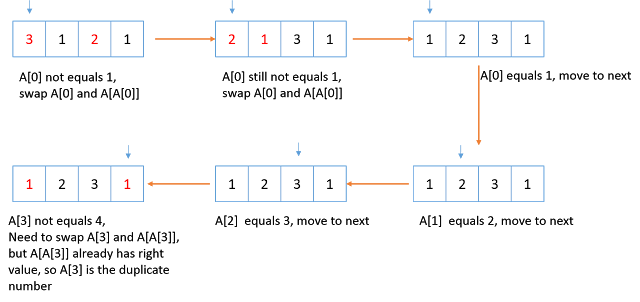
如果可以修改数组:假设数组A长度是n, 里面存储1到n的整数,那么很清楚,我们可以在按照A[i] = i+1,进行排序。但是现在有n+1个整数,而且至少有一个数字存在冗余。如果我们仍然按照A[i] = i+1来排序数组的话,那么当发现A[i]上已经是i+1的值时,说明我们已经找到了冗余数了。
public int findDup(int[] nums) {
int length = nums.length;
for(int i =0; i< length; i++) {
if(nums[i] == i+1) {
continue;
}
int newIndex = nums[i]-1;
while(nums[i] != i +1 ) {
if(nums[i] == nums[newIndex] ) {
return nums[i];
}
int temp = nums[newIndex];
nums[newIndex] = nums[i];
nums[i] = temp;
newIndex = nums[i] -1;
}
}
return -1;
}
数组有N+M个数字, 数字的范围为1 ... N, 打印重复的元素, 要求O(M + N), 空间复杂度O(1)。
a[i] != a[a[i]-1],两个互换
a[i] == a[a[i]-1],保持不变
输入a[N]到a[N+M-1] //这就是结果。
一共有N+M个数字,就把这N+M个数字放到a[o]~a[N-1]里,1 就放在 a[0]里,2就放在a[1]里, a[i]就放在a[a[i]-1]里,遍历一遍后,a[N]~a[N+M-1]放的就是重复的
public int findDup(int[] nums) {
int length = nums.length;
for(int i =0; i< length; i++) {
if(nums[i] == i+1) {
continue;
}
int newIndex = nums[i]-1;
while(nums[i] != nums[newIndex] ) {
int temp = nums[newIndex];
nums[newIndex] = nums[i];
nums[i] = temp;
newIndex = nums[i] -1;
}
}
return -1;
}